Une première approche de rationalisation concernant l'harmonie musicale

Qu'est ce qui caractérise, de manière objective, quantifiable, un accord de deux sons, deux notes, tantôt dissonantes, tantôt consonantes ? On connait la nature vibratoire du son, soit une variation rapide de la pression atmosphérique, généralement de petite amplitude. Qu'elle sont les grandeurs physiques en jeux par rapport à l'harmonie, aussi notion apparament subjective si l'en est ?

Tout commence à l'octave. L'octave dénote un rapport entre deux fréquences de notes valant 2 (ou 1/2). Exemple: le LA3 est défini aux environs de 440 Hertz [Hz], soit 440 cycles par seconde [cps], soit 440 fois par seconde ou les bras d'un diapason passent d'un écartement minimal, puis maximal, puis retour au minima.

Ainsi le LA2 vibre 220 fois par seconde, soit une fréquence de 220 Hz. Le LA1 110 Hz, le LA4 880 Hz. A noter que 55Hz est la fréquence du LA-1, le LA0 n'existant pas, par convention.

L'octave est l'accord de base après l'unisson, lui même étant simplement la superposition de deux notes identiques jouées simultanément. Il arrive parfois que l'octave soit un accord difficile à le distinguer de l'unisson selon les instruments, entre instruments passablement différents.

Aussi, les instruments graves, tels la contre-basse ou la basse électrique, enregistrés puis joués sur un dispositif de reproduction ne comportant que de petits haut-parleurs, ne seront entendu que par leurs harmoniques et non plus par leur son fondamental, celui ci descendant très souvent à une fréquence inférieure à celle reproductible par le petit haut-parleur. C'est un cas quelque peu extrême de la confusion d'une octave, de la peine à distinguer un son donné de celui à l'octave supérieur, mais devenu courant à l'air des haut-parleurs minuscule sur nos téléphones et ordinateurs portables.

Un son émis par un instrument quelconque n'est pas un son pur au sens mathématique du terme, il est toujours composé d'un son fondamental et de plusieurs harmoniques, qui sont des vibrations ou mode vibratoires en multiples entiers de la fréquence du son fondamental.

Exemple: le LA1 vibre en fondamental à 110Hz, mais sauf sur un générateur électronique, contiendra toujours un son à 220Hz, un à 330Hz, un à 440Hz, etc, ce dans un développement quasi infini, mais d'amplitude s'atténuant à mesure que l'on monte dans les harmoniques (donc les fréquences) élevées.

Le fondamental et les harmoniques sont nommés parfois des partiels. Ils sont représentables dans le temps par deux fonctions trigonométriques bien connues: le cosinus et/ou le sinus. (On rejoint par ce biais la théorie de Fourier en physique et mathématique).

Donc un son d'une note unique d'un instrument classique, acoustique, contiendra toujours une bonne part, par son harmonique de rang 2, du son de la même note jouée à l'octave supérieure.

La gamme tempérée

Le LA c'est bien joli, mais qu'en est il des autres notes, à quel fréquences vibrent-elles? L'évolution de l'accord des instruments au fil de l'histoire de la musique occidentale a aboutit à un meilleur ou moins pire compromis qui est la gamme chromatique ou gamme tempérée.

Dans cette gamme, chaque demi-ton à un rapport numérique en fréquence avec son demi-ton inférieur égal à la douzième racine de deux.

Ainsi, 12 demi-ton cumulés nous donne (2^1/12)¹² = 2, soit un rapport d'une octave.

On dit en mathématique que la séquence des fréquences des demi-ton successifs est une PROGRESSION GEOMETRIQUE.

Exemple: LA1 = 110 Hz

facteur de progression: douzième racine de deux, soit le chiffre qui élevé à la puissance 12 vaut 2:

2^1/12 = 1.05946…

Note	Fréquence
LA1	110.0 Hz
LA1#	116.5 Hz
SI1	123.5 Hz
DO2	130.8 Hz
DO2#	138.6 Hz
RE2	146.8 Hz
RE2#	155.6 Hz
MI2	164.8 Hz
FA2	174.6 Hz
FA2#	185 Hz
SOL2	196 Hz
SOL2#	207.7 Hz
LA2	220 Hz

Chacune des fréquences de ces demi-tons est séparée par un RAPPORT (notion de division ou multiplication) par son voisin de 1.059..., soit la douzième racine de deux, 2^1/12. Tel est le cas en tout cas depuis l'utilisation de la gamme chromatique.

On est plus habitué à des progressions arithmétiques, où on additionne toujours le même nombre en séquence, ici on multiplie, et c'est cela qui se nomme une progression géométrique.

Ce choix de 12 demi-ton n'est pas du au hasard, c'est un ajustement au fil de l'histoire de la musique qui débouche sur un chiffre 2^1/12 ayant quelques propriétés d'approximation d'une bonne fortune presque magique par certains de ses aspects.

Prenons le rapport entre MI2 et LA1:

MI2/LA1 = 164.8/110 = 1.498

C'est très proche de 1.5, soit 3/2.

3/2 est le rapport de fréquence de la consonance la plus forte après l'unisson et l'octave: c'est la QUINTE. Le tempérament pythagoricien est basé sur la quinte.

Essayons le rapport entre RE2 et LA1:

146.5 / 110 = 1.332

C'est cette fois très proche de 4/3, le rapport d'une autre consonance forte, la QUARTE. Toutes notes séparées de 5 demi-tons forment une consonance forte de quarte dans la gamme tempérée.

Toute ces consonances intéressantes, agréables harmoniquement, sont transposables à souhait sur toute la gamme, grace au tempérament chromatique, pour autant que l'intervalle entre et en nombres de demi-tons soit précisément respecté.

Les autres rapports de fréquences et consonances intéressant harmoniquement:

4 demi-tons, p.ex.: DO# / LA: 138.6 / 110 = 1.26, proche de 5/4, c'est la TIERCE

1 ton, SI / LA = 1.122, proche de 1.125, 9/8, c'est la SECONDE.

9 demi-tons, p.ex.: FA# / LA = 185 / 110 = 1.68, proche de 5/3. C'est peut-être celle qui perd le plus de consonance parmi celles décrites dans ce document, l'erreur entre 1.68 et 1.666666 étant relativement élevée. Si il est beaucoup utilisé dans un morceau, l'accordage peut être adapté en s'éloignant quelque peu du compromis de la gamme tempérée ou chromatique.

Tableau récapitulatif (gamme majeure héptatonique)

Note	Demi-ton	Harmonie	Rapport
DO	0	Unison	1/1
RE	2	Seconde	9/8
MI	4	Tierce	5/4
FA	5	Quarte	4/3
SOL	7	Quinte	3/2
LA	9	Sixte	5/3
SI	11	Septième	-
DO	12	Octave	2

Gamme de Zarlino

A noter que la gamme utilisant les rapports simples, 3/2, 5/4 etc. se nomme la gamme naturelle ou gamme de Zarlino. Elle sonne très bien, mais est surtout adaptable à des instrument sans frette, telle la famille des violons, ou autres instruments "fretless", sans que la précision réquise soit d'une grande évidence à atteindre.

Son demi-ton n'a pas une valeure uniforme au sein d'une octave.

Ainsi elle est nettement moins évidente à transposer et jouer en ensemble que la gamme tempérée, dont l'aspect mathématique uniforme facilite la transposition, la mise au diapason de grands ensembles, ainsi que la construction ou l'accordage d'instruments à notes fixes, piano, guitare etc…

A noter l'aspect assez extraordinaire d'approximation des ratios simple de la gamme naturelle par les multiplications successives de l'intervalle du demi-ton à la douzième racine de 2 de la gamme tempérée.

Trêve d'introduction, pourquoi ça sonne bien ?

La bonne consonance entre deux notes consiste en des rapports de fréquences pour lesquels un nombre élevé d'harmoniques (au sens mathématique) des deux notes tombes sur des fréquences IDENTIQUES ou très proche, générant qu'un battement faible, contrôlé, battement de fréquence inférieure à un tremolo

Exemple: la quinte: rapport 3/2

LA1: 110Hz Harmoniques	220 330 440 550 660 770 880 990 ... Hz
MI2: 165Hz Harmoniques	330 495 660 825 990 ... Hz

Concernant la quinte, la moitié des harmoniques de la note haute recoupe le tiers des harmoniques de la note basse.

C'est ce ratio élevé de recoupements qui explique la consonance forte de la quinte. Cette observation permet dans une bonne mesure de prévoir quels sont les consonances fortes, faibles ainsi que les dissonances.

C'est tout du moins ce sur quoi repose ce premier modèle d'explication de l'harmonie musicale. Mais ce n'est qu'un premier modèle, niveau d'explication sur la consonance. D'autres paramètres entrent en jeu, par exemple sur la guitare: la résonance de la caisse ainsi que les cordes monobrins pour les trois aiguës et bobinées pour les trois graves changent l'amplitude relative des harmoniques élevées de chaques cordes, ce qui a aussi un impact important sur la notion de consonance.

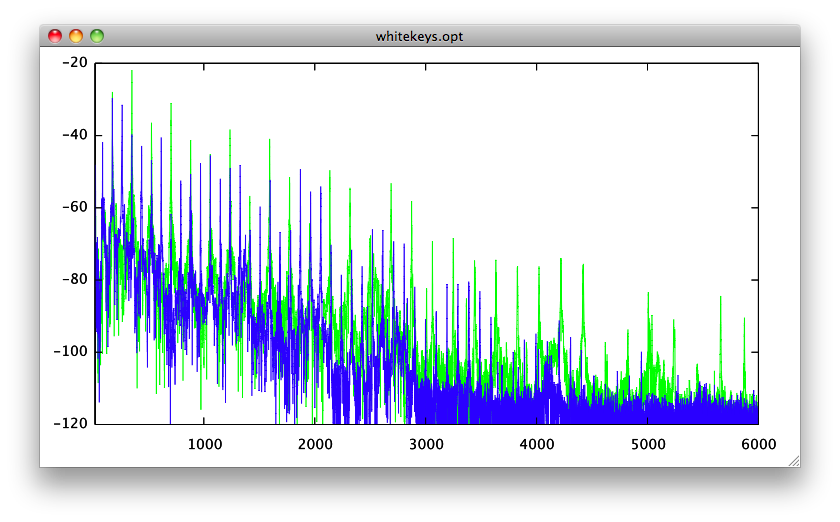
Ci-dessous, les spectres fréquentiels de deux notes séparées d'une octave au piano.

Post Scriptum (février 2024)

Une étude sur ce sujet, sur la validité de ce modèle explicatif dit Pythagoricien: https://phys.org/news/2024-02-pythagoras-wrong-universal-musical-harmonies.html